Maurer Rose Pattern

---

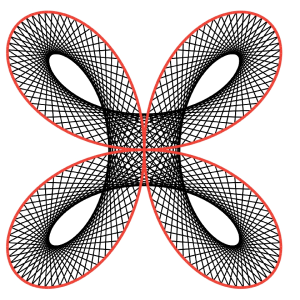
A Maurer rose of the rose $r = sin(nθ)$ consists of the 360 lines successively connecting the mentioned below 361 points, where $n$ is a positive integer. The rose has $n$ petals if $n$ is odd, and $2n$ petals if $n$ is even.
We take 361 points on the rose as:

$(sin(nk), k) (k = 0, d, 2d, 3d, ..., 360d),$
where $d$ is a positive integer and the angles are in degrees, not radians. Thus a Maurer rose is a polygonal curve with vertices on a rose.

A Maurer rose can be described as a closed route in the polar plane.

• A walker starts a journey from the origin $(0, 0)$, and walks along a line to the point $(sin(nd), d)$.
• Then, in the second leg of the journey, the walker walks along a line to the next point, $(sin(n·2d), 2d)$, and so on.
• Finally, in the final leg of the journey, the walker walks along a line, from $(sin(n·359d), 359d)$ to the ending point, $(sin(n·360d), 360d)$.
  A Maurer rose is a closed curve since the starting point, $(0, 0)$ and the ending point, $(sin(n·360d), 360d)$, coincide.

Light Mode

Dark Mode

---

Last update: December 25, 2021