Toothpick Pattern¶
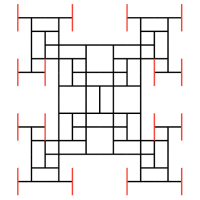
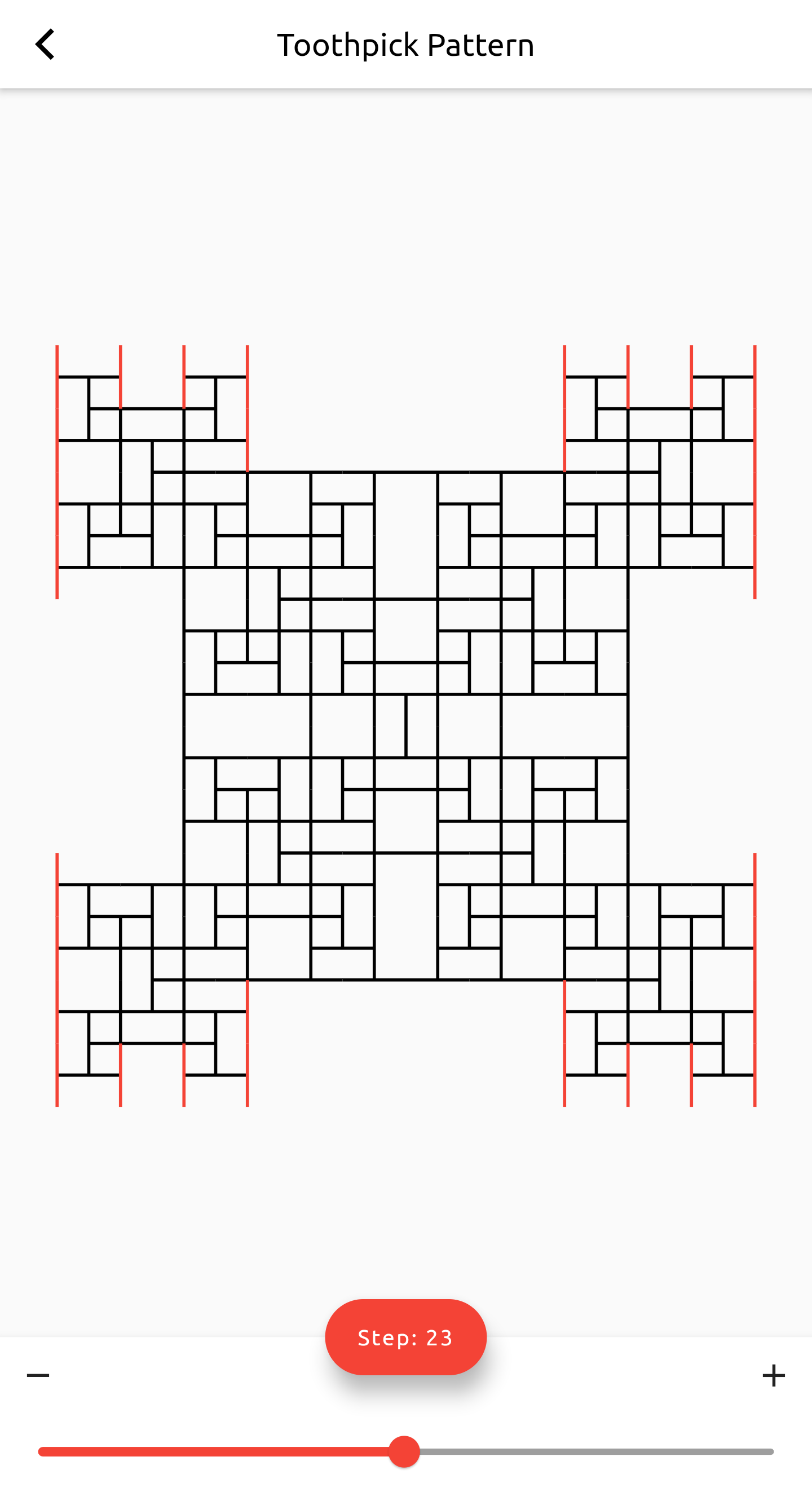
The toothpick sequence in geometry is a 2D pattern sequence which is based on the previous state of the pattern for the next stage. This is done by repeating addition of new line segments to free ends of line segments in the previous stage of the pattern. These line segments are referred to as “Toothpicks”.
The pattern begins at the first step wherein it has only one toothpick/line segment in the middle of the canvas. With each increasing step the free/exposed ends of the previous stage toothpicks are attached at right angles to the center of new toothpicks. Mathematically, this process results in a growth pattern in which the total line segments at a particular stage (n) oscillates between 0.45n2 and 0.67n2.
The pattern closely resembles the T-square fractal or the cellular arrangement in Ulam–Warburton cellular automaton1. An interesting observation is how the pattern almost forms a square at the powers of 2. The current stage in the simulation is also represented by a different colour than the rest of the pattern.

Fun Fact
The toothpick is considered such an essential that even Swiss Army knives - a popular brand of multi-function tools - have included one in their product